Pemilihan Lokasi Gudang

Read Time:4 Minute, 22 Second

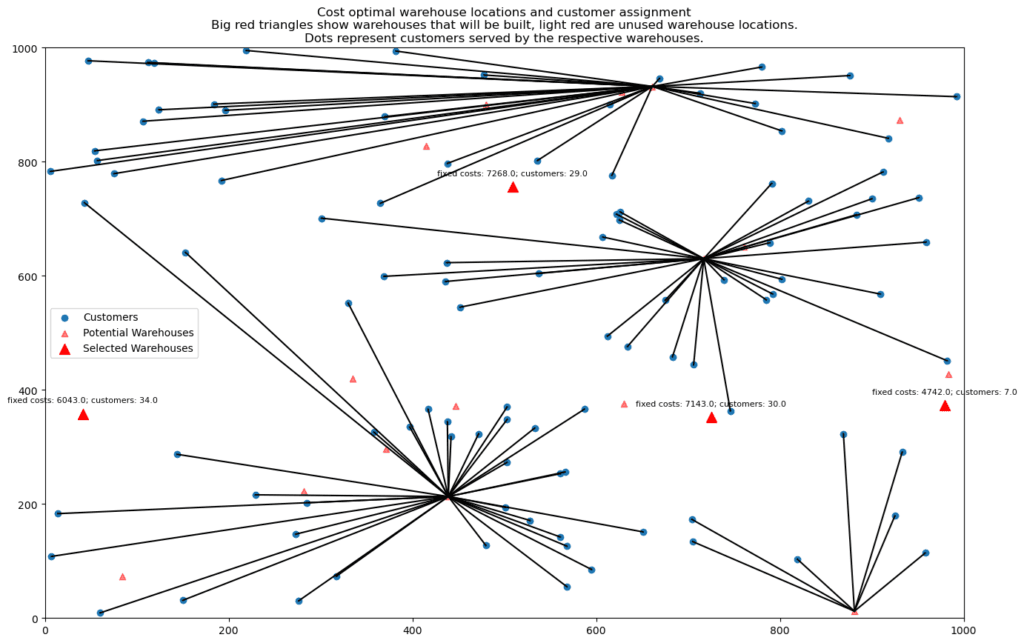
Pergudangan adalah salah satu komponen yang kurang dibicarakan dari proses rantai pasokan, tetapi ini adalah salah satu yang paling penting. Adapun masalah lokasi gudang atau warehouse location problem (WLP) adalah masalah optimasi klasik dalam operasi riset yang bertujuan menemukan lokasi optimal untuk gudang guna meminimalkan biaya transportasi sekaligus memenuhi permintaan barang dari sekelompok pelanggan. Problem ini biasanya sangat relevan untuk operasi yang perlu mendistribusikan barang ke seluruh wilayah dengan geografis yang cukup luas seperti model dibawah ini.

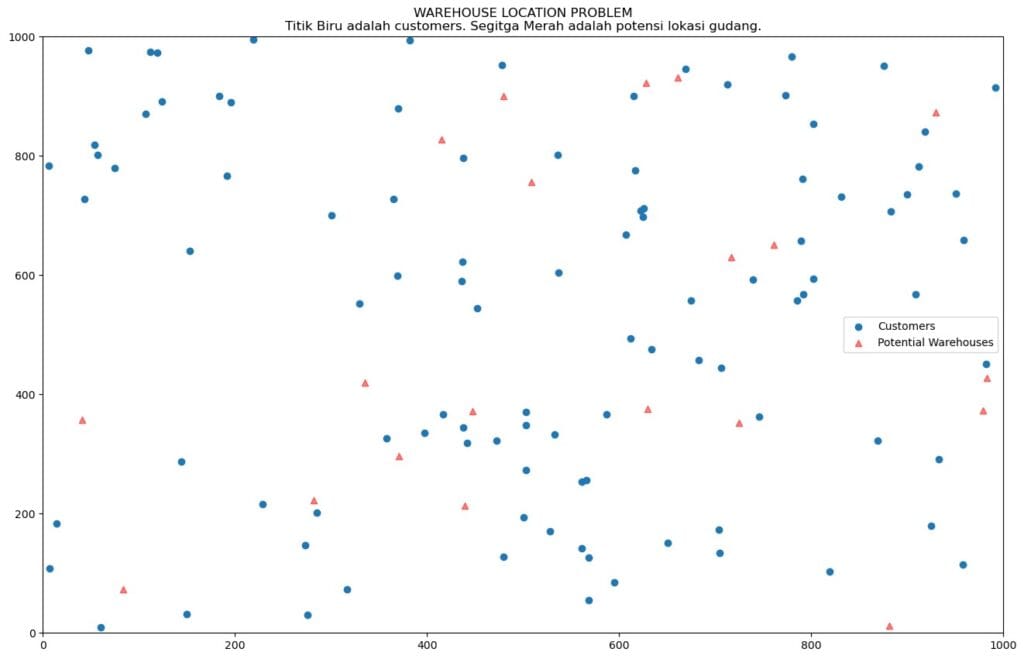
Mengingat sekumpulan pelanggan dan serangkaian lokasi untuk membangun gudang maka tugasnya adalah memutuskan di mana harus membangun gudang dan dari gudang mana barang harus dikirim ke pelanggan mana. Dengan demikian ada dua keputusan yang perlu dibuat sekaligus: dimana akan dibangun gudang dan bagaimana distribusi dari gudang itu ke pelanggan. Pengaturan sederhana ini juga menyiratkan bahwa setidaknya harus ada satu gudang yang dibangun guna melayani semua pelanggan, atau bagaimana jika harus 2 atau 3 gudang?

Model Matematika

Model matematika untuk masalah ini adalah model Mixed-Integer Linear Programming (MILP). Komponen utamanya adalah:

Variabel Keputusan:

x_i,_j adalah variabel biner yang menunjukkan apakah pelanggan i dialokasikan ke gudang j.
y_j adalah variabel biner yang menunjukkan apakah gudang j dibangun.

Fungsi Objektif:

Meminimalkan biaya total, yang mencakup biaya tetap untuk membangun gudang dan biaya transportasi:

$\boxed{min\sum_{i=1}^{n}\sum_{j=1}^{m}transportcost(i,j)\cdot x_{1,j} + \sum_{j=1}^{m}fixedcost_j \cdot y_j }$

Kendala:

Setiap pelanggan harus dialokasikan ke tepat satu gudang:

$\boxed{\sum_{j=1}^{m}x_{i,j}=1 \longrightarrow \forall i\in {\left\{1,2,...,n \right\}} }$

Gudang harus dibangun jika ada pelanggan yang dialokasikan ke sana:

$\boxed{x_{i,j}\le y_i \longrightarrow \forall i \in \left\{ 1,2,...,n \right\}, \forall j \in \left\{ 1,2,...,n \right\}}$

Batasan jumlah gudang yang akan dibangun (misalnya 3 atau 4):

$\boxed{\sum_{j=1}^{m}y_j=k }$

Perhitungan dengan menggunakan code Python

Kode program yang diimplementasikan dalam code Python menggunakan perpustakaan seperti Pandas, NumPy, Matplotlib, dan PuLP dengan mendefinisikan:

Data Lokasi:
- Lokasi pelanggan dan gudang dihasilkan secara acak (misal saja, seharusnya berdasarkan data GPS seperti lattitude dan longitude)
- Biaya tetap untuk membangun gudang dihasilkan dari distribusi normal.
Fungsi Biaya Transportasi:
- Menghitung jarak Euclidean antara pelanggan dan gudang.
Membangun Model Optimasi:
- Menetapkan fungsi objektif dan kendala.
- Memecahkan masalah menggunakan solver GLPK¹.
Menampilkan Hasil:
- Menampilkan gudang yang dipilih dan alokasi pelanggan.
- Menggambarkan hasil dalam plot visual untuk memvisualisasikan alokasi pelanggan ke gudang.

Pembahasan

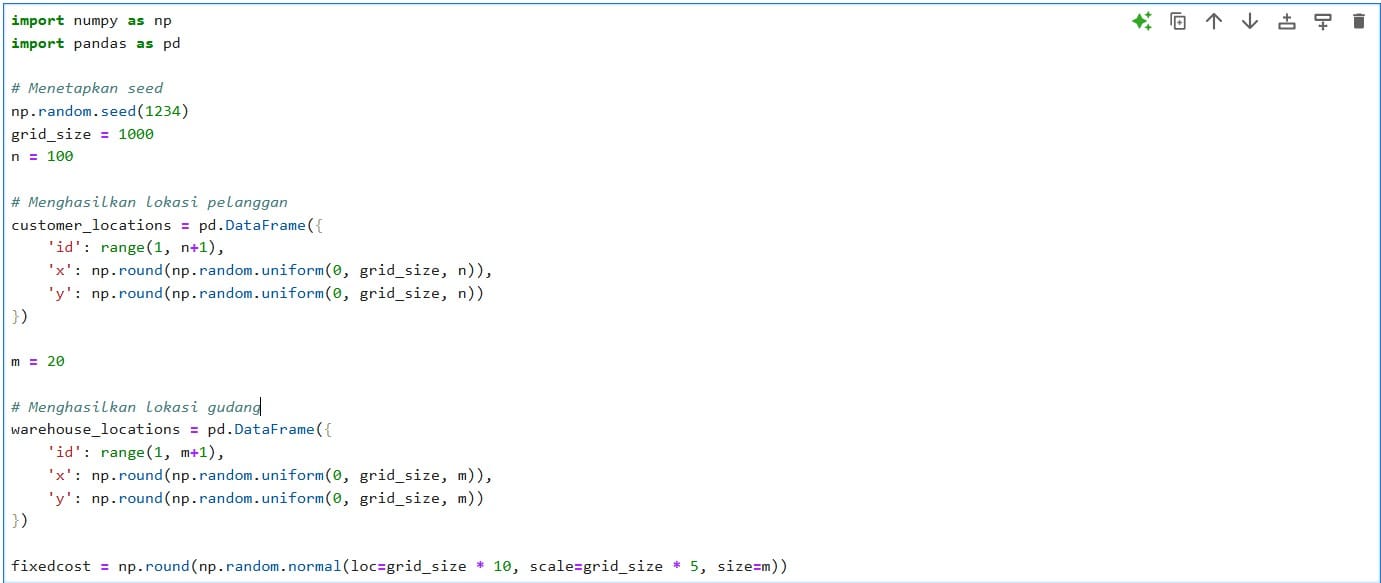
Untuk menghasilkan data lokasi dalam kode Python yang kita bahas sebelumnya, kita menggunakan Pandas dan NumPy dimana:

Menetapkan Seed: np.random.seed(1234) untuk memastikan hasil yang dihasilkan bisa direproduksi.
Ukuran Grid: grid_size adalah 1000, yang menentukan ukuran grid.
Jumlah Pelanggan: n adalah 100, yang menentukan jumlah pelanggan.
Menghasilkan Lokasi Pelanggan: Lokasi pelanggan dihasilkan secara acak dalam grid dengan menggunakan np.random.uniform dan disimpan dalam dataframe customer_locations.
Jumlah Gudang: m adalah 20, yang menentukan jumlah lokasi gudang potensial.
Menghasilkan Lokasi Gudang: Lokasi gudang dihasilkan secara acak dalam grid dengan menggunakan np.random.uniform dan disimpan dalam dataframe warehouse_locations.
Biaya Tetap: fixedcost dihasilkan dari distribusi normal menggunakan np.random.normal.

Bagian kode di atas adalah dasar untuk menghasilkan data lokasi yang kemudian digunakan dalam pemodelan dan optimasi. Adapun kode untuk fungsi biaya transportasi adalah:

Dimana:

Fungsi: transportcost(i, j) mengembalikan biaya transportasi antara pelanggan i dan gudang j.
Pengambilan Data Pelanggan dan Gudang: customer = customer_locations.iloc[i] dan warehouse = warehouse_locations.iloc[j] mengambil lokasi pelanggan dan gudang berdasarkan indeks ii dan jj.
Menghitung Jarak Euclidean: math.sqrt((customer['x'] - warehouse['x'])**2 + (customer['y'] - warehouse['y'])**2) menghitung jarak Euclidean antara pelanggan dan gudang.
Pembulatan: round() digunakan untuk membulatkan hasil jarak ke bilangan bulat terdekat.

Contoh penggunaan fungsi print(transportcost(0,2)) adalah untuk encetak biaya transportasi antara pelanggan pertama (indeks 0) dan gudang ketiga (indeks 2).

Berikut adalah kode untuk model optimasi yang digunakan untuk masalah lokasi gudang. Kode ini mendefinisikan model optimasi menggunakan perpustakaan PuLP di Python dan menyertakan fungsi objektif serta kendala:

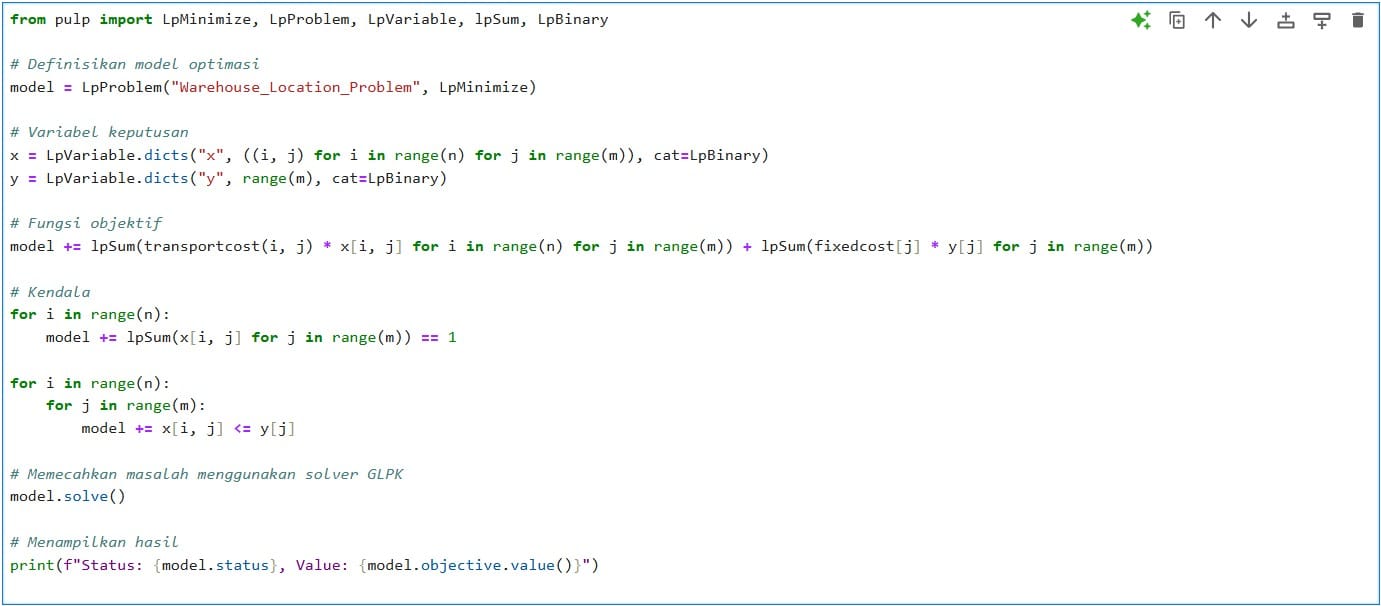
Dengan menggunakan model MILP, kita dapat menentukan lokasi optimal untuk mendirikan gudang dan mengalokasikan pelanggan dengan efisien. Model ini mempertimbangkan biaya tetap dan biaya transportasi untuk meminimalkan biaya total. Mixed-Integer Linear Programming (MILP) berfungsi memecahkan masalah LP (Optimasi Linier) dengan variabel integer, yang memungkinkan untuk model yang lebih kompleks seperti masalah lokasi gudang diatas.

Hasil:

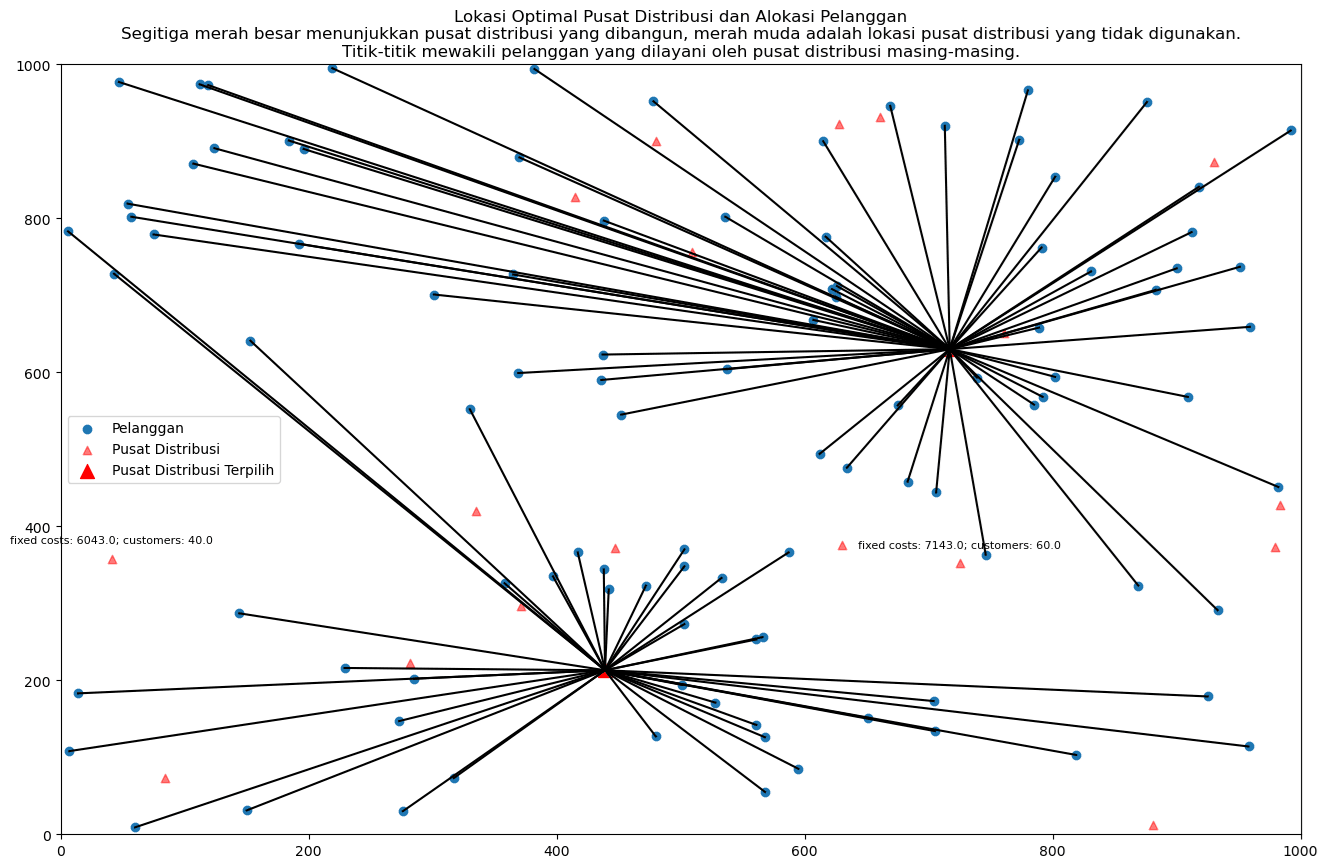
Jika mengharuskan ada lebih dari hasil optimal yang sudah dipilih oleh model (seperti output diatas), maka code dapat dimodifikasi jika jumlah gudang dialokasikan, misalnya 3 gudang atau 4 gudang yang akan digunakan. Maka codingnya seperti dibawah ini.

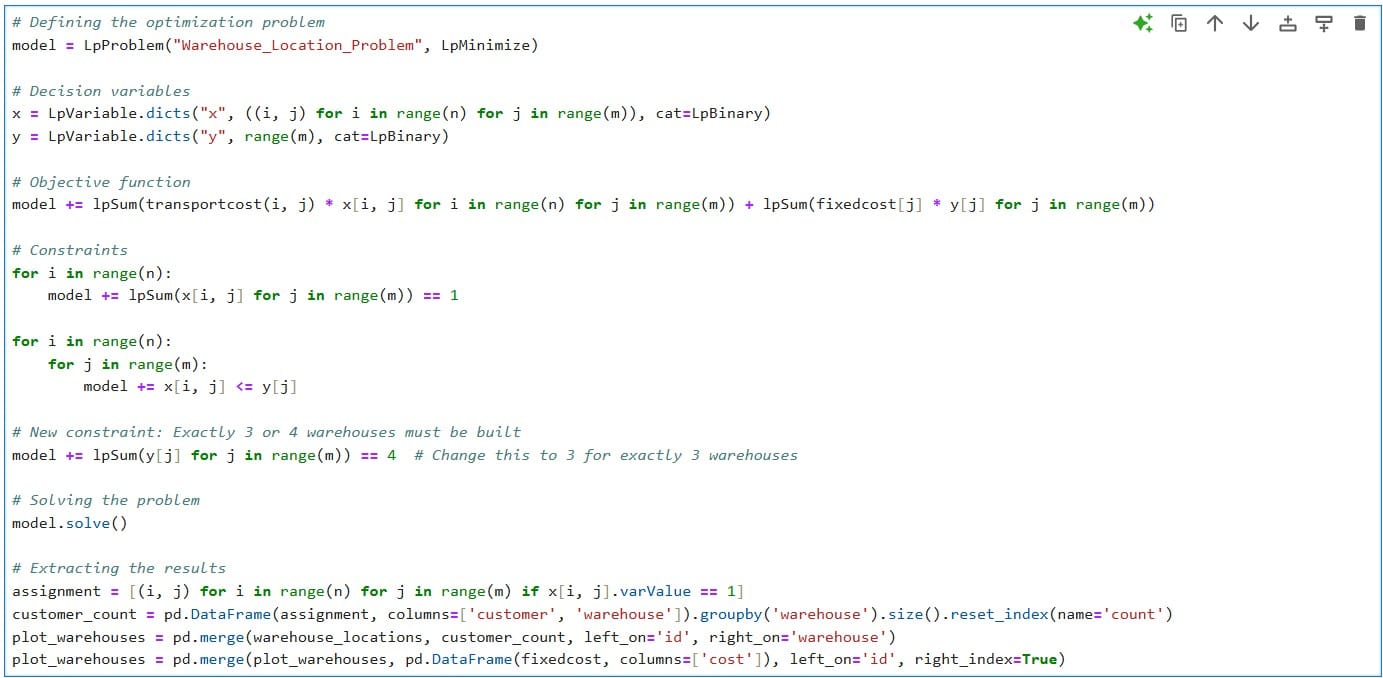
Dalam contoh di atas, batasan lpSum(y[j] for j in range(m)) == 4 memastikan bahwa tepat ada 4 gudang yang akan dibangun. Nilai ini dapat diubah menjadi 3 jika jika diinginkan tepat ada 3 gudang.

Untuk plot hasil seperti dibawah ini.

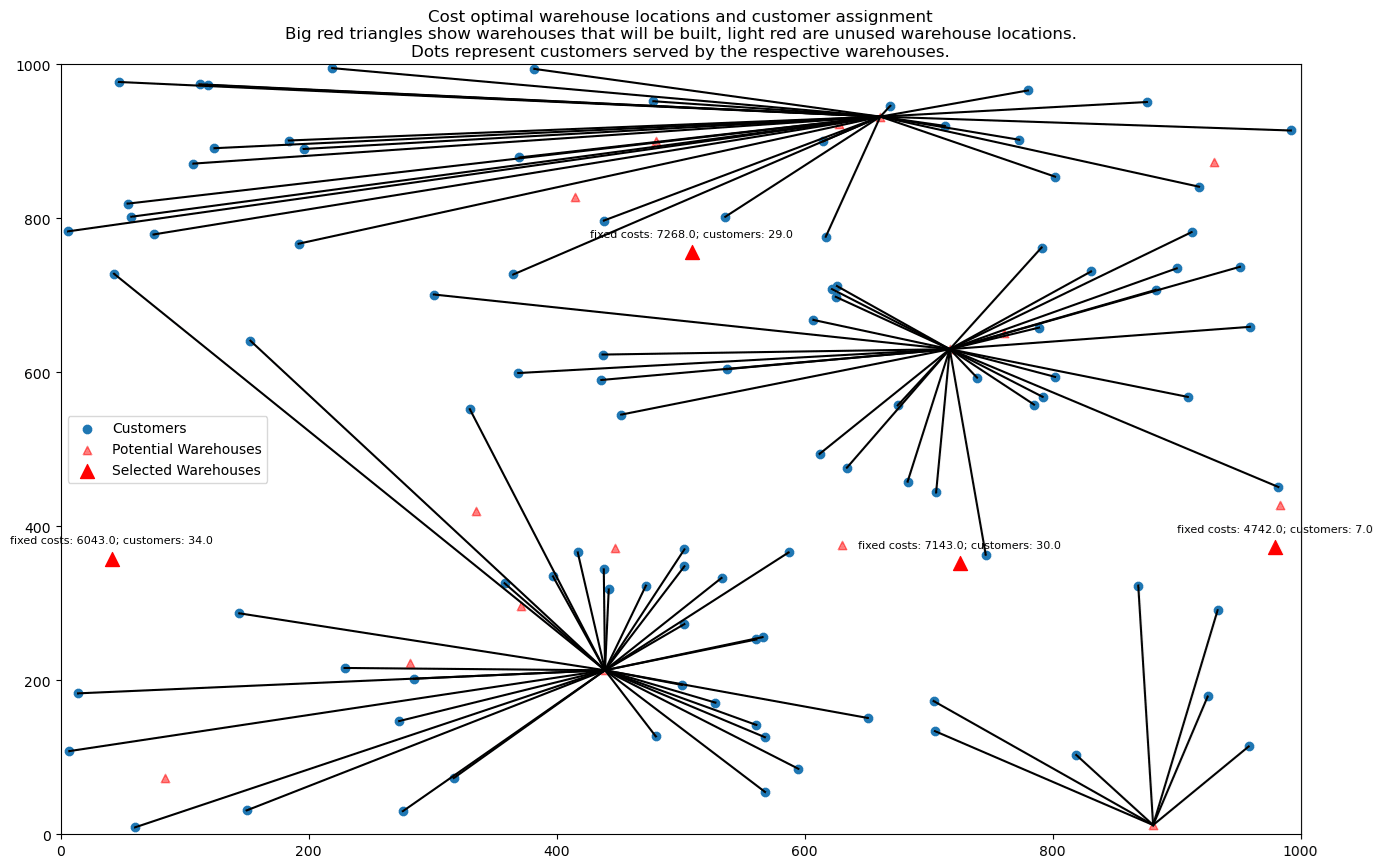
Selamat Mencoba!

About Post Author

Muh. Burhanuddin

Industrial Engineer, Specialist in Heavy Cargo Transportation and Heavy Lifting Works. Hobby in computer programming, reading and writing. No occupation except waiting for a prayer time. Ready for working as a surveyor, transport planer, or as lifting engineer.

muh.burhanuddin@live.com

https://www.alvinburhani.net

Happy

0 %

Sad

0 %

Excited

100 %

Sleepy

0 %

Angry

0 %

Surprise

0 %

About The Author

Muh. Burhanuddin

See author's posts

GLPK, atau GNU Linear Programming Kit, adalah perangkat lunak open-source yang dirancang untuk memecahkan masalah optimasi linear dan mixed-integer linear programming (MILP). GLPK menyediakan solver yang efisien dan dapat digunakan dalam berbagai aplikasi, termasuk logistik, perencanaan, dan alokasi sumber daya.